Saturday 27 October 2012
Tuesday 9 October 2012
EXERCISE YOURSELF
2D SHAPE
1] What is the name of this shape ?
A]octagon B]nonagon
C]decagon D]hexagon
2]How many symmetry lines in
equilateral triangle?
A]0 B]1 C]2 D]3
3]How many lines in semi-circle?
A]1 B]2 C]0 D]4
PERIMETER
1]Diagram 1 shows a square
.
6cm
What is the perimeter of diagram 1?
A]12cm B]18cm
C]24cm D]21cm
2]diagram 2 shows an equilateral triangle and
a square.
If the perimeter of a square is
7cm,what is the perimeter of
an equilateral triangle and 2
square?
3]diagram 3 shows a square
9cm
what is the perimeter of 0.5 of diagram 3?
AREA
1]diagram 1 shows a square.
what is the perimeter of diagram?
2]what is the area of 3 shape below?
12cm
3]diagram 2 shows a rectangle and a square.
5m
3.5m
what is the difference between the square and the rectangle?
3D shape
1]what is the shape of this net?
2]- Has 4 triangular flat face and a
square flat face
what is the name of the shape
based on the information above?
volume
1]Diagram 1 shows a cube.The perimeter of 1 side of diagram 1 is 30cm.What is the volume of
diagram 1?
2]diagram 2 shows a cuboid.the length is 12cm.the height is 5cm less than the length.what is the volume of diagram 2?
3cm
Monday 8 October 2012
SHAPE
This article is about describing the shape of an object. For common shapes, see list of geometric shapes. For other uses, see Shape (disambiguation).
The shape (Old English: gesceap, created thing)
of an object located in some space is a geometrical description of the
part of that space occupied by the object, as determined by its external
boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material composition.Mathematician and statistician David George Kendall writes:[1]
In this paper ‘shape’ is used in the vulgar sense, and means what one would normally expect it to mean. [...] We here define ‘shape’ informally as ‘all the geometrical information that remains when location, scale[2] and rotational effects are filtered out from an object.’Simple shapes can be described by basic geometry objects such as a set of two or more points, a line, a curve, a plane, a plane figure (e.g. square or circle), or a solid figure (e.g. cube or sphere). Most shapes occurring in the physical world are complex. Some, such as plant structures and coastlines, may be so arbitrary as to defy traditional mathematical description – in which case they may be analyzed by differential geometry, or as fractals.
In geometry, two subsets of a Euclidean space have the same shape if one can be transformed to the other by a combination of translations, rotations (together also called rigid transformations), and uniform scalings. In other words, the shape of a set of points is all the geometrical information that is invariant to translations, rotations, and size changes. Having the same shape is an equivalence relation, and accordingly a precise mathematical definition of the notion of shape can be given as being an equivalence class of subsets of a Euclidean space having the same shape.
Shapes of physical objects are equal if the subsets of space these objects occupy satisfy the definition above. In particular, the shape does not depend on the size and placement in space of the object. For instance, a "p" and a "d" have the same shape, as they can be perfectly superimposed if the "p" is translated to the right by a given distance, rotated upside down and magnified by a given factor (see Procrustes superimposition for details). However, a mirror image could be called a different shape. For instance, a "b" and a "d" have a different shape, at least when they are constrained to move within a two-dimensional space like the page on which they are written. Even though they have the same size, there's no way to perfectly superimpose them by traslating and rotating them along the page. Similarly, within a three-dimensional space, a right hand and a left hand have a different shape, even if they are the mirror images of each other. Shapes may change if the object is scaled non uniformly. For example, a sphere becomes an ellipsoid when scaled differently in the vertical and horizontal directions. In other words, preserving axes of symmetry (if they exist) is important for preserving shapes. Also, shape is determined by only the outer boundary of an object. For example, a solid ice cube and a second ice cube containing an inner cavity (air bubble) have the same shape.[citation needed]
Objects that can be transformed into each other by rigid transformations and mirroring are congruent. An object is therefore congruent to its mirror image (even if it is not symmetric), but not to a scaled version. Objects that have the same shape or one has the same shape as the other's mirror image (or both if they are themselves symmetric) are called geometrically similar. Thus congruent objects are always geometrically similar, but geometrical similarity additionally allows uniform scaling.
THE STORY OF MATHS
The Story of Maths is a four-part British television series outlining aspects of the history of mathematics. It was a co-production between the Open University and the BBC and aired in October 2008 on BBC Four. The material was written and presented by University of Oxford professor Marcus du Sautoy.[1] The consultants were the Open University academics Robin Wilson, professor Jeremy Gray and June Barrow-Green. Kim Duke is credited as series producer.[2]
The series comprised four programmes respectively titled: The Language of the Universe; The Genius of the East; The Frontiers of Space; and To Infinity and Beyond. Du Sautoy documents the development of mathematics covering subjects such as the invention of zero and the unproven Riemann hypothesis, a 150 year old problem for whose solution the Clay Mathematics Institute has offered a $1,000,000 prize. He escorts viewers through the subject's history and geography. He examines the development of key mathematical ideas and shows how mathematical ideas underpin the world's science, technology, and culture.
He starts his journey in ancient Egypt and finishes it by looking at current mathematics. Between he travels through Babylon, Greece, India, China, and the medieval Middle East. He also looks at mathematics in Europe and then in America and takes the viewers inside the lives of many of the greatest mathematicians.
In this opening programme Marcus du Sautoy looks at how important and fundamental mathematics is to our lives before looking at the mathematics of ancient Egypt, Mesopotamia, and Greece.
Du Sautoy commences in Egypt where recording the patterns of the seasons and in particular the flooding of the Nile was essential to their economy. There was a need to solve practical problems such as land area for taxation purposes.[3] Du Sautoy discovers the use of a decimal system based on the fingers on the hands, the unusual method for multiplication and division. He examines the Rhind Papyrus, the Moscow Papyrus and explores their understanding of binary numbers, fractions and solid shapes.
He then travels to Babylon and discovered that the way we tell the time today is based on the Babylonian 60 base number system. So because of the Babylonians we have 60 seconds in a minute, and 60 minutes in an hour. He then shows how the Babylonians used quadratic equations to measure their land. He deals briefly with Plimpton 322.
In Greece, the home of ancient Greek mathematics, he looks at the contributions of some of its greatest and well known mathematicians including Pythagoras, Plato, Euclid, and Archimedes, who are some of the people who are credited with beginning the transformation of mathematics from a tool for counting into the analytical subject we know today. A controversial figure, Pythagoras’ teachings were considered suspect and his followers seen as social outcasts and a little be strange and not in the norm. There is a legend going around that one of his followers, Hippasus, was drowned when he announced his discovery of irrational numbers. As well as his work on the properties of right angled triangles, Pythagoras developed another important theory after observing musical instruments. He discovered that the intervals between harmonious musical notes are always in whole number intervals.[4] It deals briefly with Hypatia of Alexandria.
The series comprised four programmes respectively titled: The Language of the Universe; The Genius of the East; The Frontiers of Space; and To Infinity and Beyond. Du Sautoy documents the development of mathematics covering subjects such as the invention of zero and the unproven Riemann hypothesis, a 150 year old problem for whose solution the Clay Mathematics Institute has offered a $1,000,000 prize. He escorts viewers through the subject's history and geography. He examines the development of key mathematical ideas and shows how mathematical ideas underpin the world's science, technology, and culture.
He starts his journey in ancient Egypt and finishes it by looking at current mathematics. Between he travels through Babylon, Greece, India, China, and the medieval Middle East. He also looks at mathematics in Europe and then in America and takes the viewers inside the lives of many of the greatest mathematicians.
In this opening programme Marcus du Sautoy looks at how important and fundamental mathematics is to our lives before looking at the mathematics of ancient Egypt, Mesopotamia, and Greece.
Du Sautoy commences in Egypt where recording the patterns of the seasons and in particular the flooding of the Nile was essential to their economy. There was a need to solve practical problems such as land area for taxation purposes.[3] Du Sautoy discovers the use of a decimal system based on the fingers on the hands, the unusual method for multiplication and division. He examines the Rhind Papyrus, the Moscow Papyrus and explores their understanding of binary numbers, fractions and solid shapes.
He then travels to Babylon and discovered that the way we tell the time today is based on the Babylonian 60 base number system. So because of the Babylonians we have 60 seconds in a minute, and 60 minutes in an hour. He then shows how the Babylonians used quadratic equations to measure their land. He deals briefly with Plimpton 322.
In Greece, the home of ancient Greek mathematics, he looks at the contributions of some of its greatest and well known mathematicians including Pythagoras, Plato, Euclid, and Archimedes, who are some of the people who are credited with beginning the transformation of mathematics from a tool for counting into the analytical subject we know today. A controversial figure, Pythagoras’ teachings were considered suspect and his followers seen as social outcasts and a little be strange and not in the norm. There is a legend going around that one of his followers, Hippasus, was drowned when he announced his discovery of irrational numbers. As well as his work on the properties of right angled triangles, Pythagoras developed another important theory after observing musical instruments. He discovered that the intervals between harmonious musical notes are always in whole number intervals.[4] It deals briefly with Hypatia of Alexandria.
Sunday 7 October 2012
3-D SHAPE
3-D SHAPE
THESE ARE ALL3-D SHAPE

VOLUME
FORMULA FOR VOLUME IS:
LENGTH x BREADTH x HEIGHT=_____CM3/M3
OR
AREA x HEIGHT=______CM3/M3
EXAMPLE FOR CUBE IS:

6CM
DIAGRAM 1 SHOWS A CUBE.
FIND THE VOLUME.
THE ANSWER IS:6CMx6CMx6CM
=216CM3.
SURFACE AREA
FORMULA FOR SURFACE AREA IS:
(____CM/M x ____CM/M) x ___ +
(____CM/M x____CM/M) x____=ANSWER
EXAMPLE:

DIAGRAM 2 SHOWS A CUBE
FIND THE SURFACE AREA FOR TIHS CUBE.
THE ANSWER IS:6CM x 6CM x 6= 216CM.
THESE ARE ALL3-D SHAPE
VOLUME
FORMULA FOR VOLUME IS:
LENGTH x BREADTH x HEIGHT=_____CM3/M3
OR
AREA x HEIGHT=______CM3/M3
EXAMPLE FOR CUBE IS:

6CM
DIAGRAM 1 SHOWS A CUBE.
FIND THE VOLUME.
THE ANSWER IS:6CMx6CMx6CM
=216CM3.
SURFACE AREA
FORMULA FOR SURFACE AREA IS:
(____CM/M x ____CM/M) x ___ +
(____CM/M x____CM/M) x____=ANSWER
EXAMPLE:

DIAGRAM 2 SHOWS A CUBE
FIND THE SURFACE AREA FOR TIHS CUBE.
THE ANSWER IS:6CM x 6CM x 6= 216CM.
Friday 5 October 2012
2-D shape
THE 2-D SHAPE
THESE ARE ALL 2-D SHAPE AND ITS SIDE:
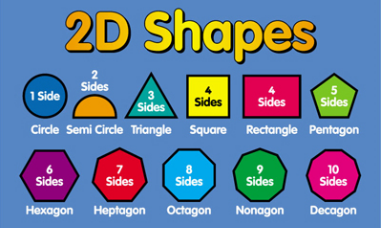
THERE ARE 3 TYPES OF TRIANGLE:
:
RIGHT ANGLE TRIANGLE

EQUILATERAL TRIANGLE
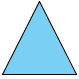
ISOSCELES TRIANGLE
PERIMETER
THE EXAMPLE IS:
10CM 1OCM
1OCM
7CM
PERIMETER:7CM+10CM+10CM
=27CM
AREA
THE EXAMPLE IS:
8CM
8CM 8CM
8CM
8CM
AREA:8CMx8CM
=64CM2
THE FORMULA OF TAHE AREA IS:
LENGTH(CM)xWIDTH(CM)=_____CM2
THESE ARE ALL 2-D SHAPE AND ITS SIDE:

THERE ARE 3 TYPES OF TRIANGLE:
:
RIGHT ANGLE TRIANGLE

EQUILATERAL TRIANGLE

ISOSCELES TRIANGLE
PERIMETER
THE EXAMPLE IS:
10CM
 1OCM
1OCM 7CM
PERIMETER:7CM+10CM+10CM
=27CM
AREA
THE EXAMPLE IS:
8CM
8CM
 8CM
8CM 8CM
AREA:8CMx8CM
=64CM2
THE FORMULA OF TAHE AREA IS:
LENGTH(CM)xWIDTH(CM)=_____CM2
Subscribe to:
Posts (Atom)



